Curva a campana di Gauss
La Curva a campana di Gauss è la distribuzione normale delle probabilità, è la modalità normale del manifestarsi di qualsiasi fenomeno naturale: dalla misura del torace dei soldati scozzesi, alla statura dei militari di leva francesi che lo statistico belga Quételet per primo osservò.
Proprietà della Curva a campana di Gauss
Il valore medio, cioè quello che corrisponde alla media aritmetica delle rilevazioni è quello che presenta la frequenza maggiore, quindi si trova nel punto più alto della curva.
La curva è simmetrica, quasi speculare, rispetto alla media centrale, difatti si parla anche di distribuzione a ogiva.
Attorno alla media, quindi nella zona più convessa della curva, ci sono le misure più frequenti.
Es la misura del torace e dell’altezza in cm
| n° toraci | cm torace | n°altezze | cm altezza | |
| 1 | 65-70 | 1 | 150-155 | |
| 2 | 70-75 | 2 | 155-160 | |
| 3 | 75-80 | 3 | 160-165 | |
| 4 | 80-85 | 4 | 165-170 | |
| 5 | 85-90 | 5 | 170-175 | |
| 4 | 90-95 | 4 | 175-180 | |
| 3 | 95-100 | 3 | 180-185 | |
| 2 | 100-105 | 2 | 185-190 | |
| 1 | 105-110 | 1 | 190-195 |
La relazione tra la curva normale e la deviazione standard
Nella curva di Gauss il 68,3% delle misure effettuate sta tra le due deviazioni standard (una positiva e una negativa) dalla media.
Il 95,4% delle misure effettuate sta il doppio delle due deviazioni standard dalla media.
Il 99,7% delle misure effettuate sta il triplo delle due deviazioni standard dalla media.

Al crescere del numero di deviazione standard, la probabilità di essere all’interno della campana si avvicina sempre più al 100%, mentre la probabilità di essere fuori si avvicina sempre più allo zero.
La media mediana e moda nella curva normale gaussiana
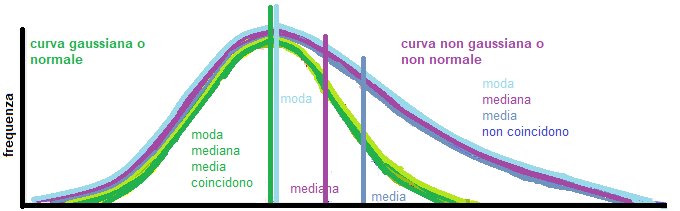
Nella curva gaussiana la moda, la mediana e la media coincidono, la media la moda e la mediana si trovano esattamente al centro della curva.
La media è il valore medio pari alla media aritmetica delle misure fatte.
La mediana è il valore che sta a metà strada esatta nella distribuzione delle misure fatte.
La moda è il valore più presente delle misure fatte.
Ancora sulla curva gaussiana
La distribuzione è normale se è completamente entro 3 deviazioni standard positive o negative.
Quando la distribuzione si limita a 3ds si dice che ha curtosi 3.
La distribuzione dopo 2ds si dice coda.
Se la distribuzione ha curtosi maggiore di 3 ha più massa nelle code, cioè le code sono spesse. Una distribuzione a code spessa è detta distribuzione leptocurtica.
La distribuzione statistica può essere simmetrica (0) come abbiamo appena visto o asimmetrica (>0<).
La curva non gaussiana o curva non normale
Ovviamente ci sono anche distribuzione non normali, cioè non simmetriche.

Nella donna la durata della gestazione fino al parto forma una curva a campana, ma non certo una curva gaussiana.
La curva gaussiana nella distribuzione della ricchezza
Pareto ha studiato nelle scienze sociali la curva gaussiana e ha osservato che in questo campo essa non funziona.
Il divario tra ricchi e poveri è sempre esistito. L’intuito fa pensare a una distribuzione piramidale oppure se crediamo alla democrazia che la distribuzione sia perfettamente gaussiana o normale. Pareto la misurò e trovò invece una campana asimmetrica. Su un asse il reddito e sull’altro il numero di persone con i diversi redditi, in paesi diversi e in epoche diverse disegna sempre la curva estremamente asimmetrica vista per la prima volta da Pareto. La distribuzione del reddito può essere anche vista con gli occhi della teoria dei giochi. La teoria dei giochi dimostra che in una società possono esserci pochi ricchi e una infinità di poveri, come in natura ci sono pochi falchi aggressivi e molte colombe remissive. In natura troppi falchi sarebbero sempre in lotta fra loro, mentre le colombe vivono e lasciano vivere. Questo allora fa pensare che i nuovi ricchi sono arroganti come i falchi ? Vediamo che Pareto e Nash sono concordi.
